1.1 Simulated Flow

Contents

Index

1.1 Simulated Flow

Vertical accelerations of the fluid are neglected, which allows to integrate the remaining part of the vertical momentum equation and to obtain an expression for the pressure which in turn can then be eliminated from the system. The error associated with this approximation is of the order of -d(p)/dx/(rho*u_t)~h²/l² (h undisturbed water height, l characteristic length scale of the waves in x-direction). This estimate is equivalent to the so-called "long-wave limit" of wave motion, i.e. we are dealing with either very long waves or with shallow water. Physically, the horizontal velocity that is retained can be interpreted as a vertical average of the fluid velocity.

Schematic of the coordinates and variables of the shallow water model

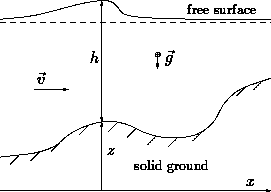
The system of equations that governs the above class of flows can be conveniently written as follows:

where

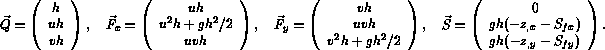
In the above notation, h signifies the water depth, u and v the horizontal velocity coordinates of the fluid, g the gravitational accelaration, z the vertical coordinate of the bottom taken from some reference point, S_fx and S_fy denote the two components of the bottom friction that can be expressed by the Manning formula

where n is an empirical roughness coefficient.

1.1 Simulated Flow

Contents

Index