Contents
| | | 4 Weak solutions of conservation laws and the jump conditions | Contents | Index |
The present account follows that of Smoller [5]. We consider the initial value problem for a conseration law
The test function phi used during the derivation of
the class of weak solutions of system
(4) (left) and the notation for the
solution of a jump discontinuity around the point P on the
curve Gamma (right).
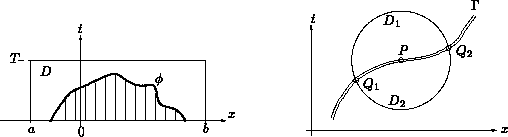
Let us define a test function phi(x,t) which vanishes outside of a compact support and particularly on t=T, x=a and x=b (cf. figure 4). Multiplication of (4) by phi(x,t) and integration for t>0 over a domain D gives:
Integration by parts of the time derivative in (4)
and of the spatial derivative
leads to:
A bounded measurable function u(x,t) is called a weak solution of the initial-value problem (4) with bounded and measurable initial data u0 provided that (4) holds for all phiin C01. If u is continuous C1, then (4) describes a classical solution of (4).
Turning now to the jump conditions, let Gamma(x,t) be a smooth curve across which u(x,t) has a jump discontinuity (i.e. a discontinuity in the zeroth derivative). Consider a domain D around some point P on Gamma (cf. figure 4 b); phi(x,t) is a continuous test function with support centered at P and - as above - zero on the boundaries of D. A weak solution on the domain D satisfies
Since u(x,t) is continuous on both sides of Gamma, i.e. in D1, D2 one can use the divergence theorem
markus.uhlmann AT ciemat.es
| | | 4 Weak solutions of conservation laws and the jump conditions | Contents | Index |
