3.2 Godunov's scheme

Contents

Index

3.2 Godunov's scheme

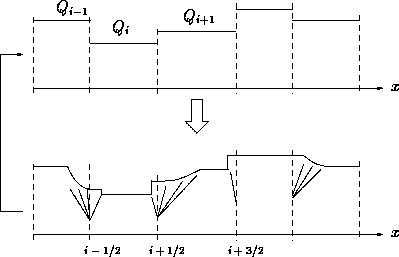
The steps of Godunov's scheme for solving a one-dimensional hyperbolic problem: discretization into cell-wise constant values; exact solution of the ensueing Riemann problems at the cell-interfaces (subject to a CFL-like condition); subsequent averaging over the cells.

The idea behind Godunov's method (cf. [8]) consists in solving analytically the Riemann problems arising at each cell interface of a cell-wise constant finite-volume scheme (figure). The obtained solution is again cell-averaged before the following time step. As such, Godunov's scheme is a finite volume method

where the numerical flux function F^G is the physical flux computed from the exact solution Q^R of the individual Riemann problem, taken at the location of the cell-interface, viz.

In practice, this means that Q^R is the value of the solution of the respective Riemann problem at xi=0 in local coordinates. For the shallow water equations, this is simply the center state Q_c of the interaction (cf. figure) which we have calculated in §2.2. With a few additions, the routine given in appendix can thus be transformed into a Godunov solver (see appendix).

In Godunov's scheme a restriction of the permissible time step arises from the condition that neighboring Riemann problems do not interact, i.e. that the maximum signal velocities do not cover more than half a cell-dimension during a time interval, viz.

and sigma only makes sense in the presence of a shock in the ith cell.

The Godunov method is overall monotone, i.e. does not give rise to oscillations in the presence of discontinuities, and it is of formal first order accuracy in time and space. Moreover, the scheme has the important property of respecting the entropy condition (cf. §2.2) that guarantees a physically meaningful solution. This fact is not surprising since the essential physics of the underlying system are built into the numerical method.

Why, then, is this method not largely utilized in practice? Basically, it can become quite time-consuming due to the iterative solution of each Riemann problem. Moreover, the great detail of the cell-wise solution is partially lost during the averaging stage so that a simplified approach is often sufficient.

3.2 Godunov's scheme

Contents

Index